Δευτέρα 21 Δεκεμβρίου 2015
Δευτέρα 16 Νοεμβρίου 2015
Τετάρτη 4 Νοεμβρίου 2015
Στερεό, κρούση, στροφορμή, ταλάντωση
Στο λείο οριζόντιο δάπεδο ταλαντεύεται η σανίδα του σχήματος
που έχει μάζα 2kg.
Όταν βρίσκεται στην θέση ισορροπίας της ταλάντωσης πέφτει
κατακόρυφα μία μπάλα μάζας 10kg και ακτίνας 10cm με ταχύτητα 5m/s.
Ο συντελεστής τριβής μεταξύ μπάλας και σανίδας είναι 0,1.
Οι παραμορφώσεις των σωμάτων είναι ελαστικές και η σανίδα
δεν αναπηδά στο δάπεδο.
Βρείτε την γωνία ανάκλασης της μπάλας και το νέο πλάτος
ταλάντωσης της σανίδας.
Δίδεται ότι η επιτάχυνση της βαρύτητας έχει την συνήθη
ασκησιακή της τιμή.
Σάββατο 31 Οκτωβρίου 2015
Θα υπάρξει ολίσθηση;
Ένα σώμα Α μάζας m αφήνεται να κινηθεί πάνω σε σανίδα
μάζας Μ. Ο συντελεστής οριακής στατικής τριβής μεταξύ σώματος Α και σανίδας
είναι μ=0,8∙εφφ, όπου φ η κλίση του λείου κεκλιμένου επιπέδου, ενώ το κεκλιμένο επίπεδο είναι λείο.
i)
Στο πρώτο σχήμα η σανίδα συγκρατείται από εμάς και αφήνεται ταυτόχρονα με το
σώμα Α.
ii)
Στο δεύτερο σχήμα, η σανίδα ηρεμεί στο άκρο ελατηρίου.
Θα υπάρξει ολίσθηση του σώματος Α πάνω στη σανίδα τη στιγμή που αφήνεται να κινηθεί και αν ναι, σε ποια περίπτωση;
Ετικέτες
5. Θεωρία,
9. Δυναμική,
Διονύσης Μάργαρης
Σάββατο 24 Οκτωβρίου 2015
Νόμος του Poiseuille για σωλήνα.
Μια μόνιμη και στρωτή ροή πραγματικού
ρευστού.
Έστω σε ένα οριζόντιο σωλήνα,
κυλινδρικού σχήματος, ακτίνας R και μήκους
, έχουμε μια μόνιμη και στρωτή ροή, ενός πραγματικού ρευστού
με συντελεστή ιξώδους n.
Η ροή ονομάζεται μόνιμη, αφού σε κάθε σημείο, η
ταχύτητα έχει μια συγκεκριμένη τιμή ανεξάρτητη του χρόνου και στρωτή, αφού ναι μεν η ταχύτητα είναι διαφορετική στα
διάφορα σημεία μιας τομής, αλλά μπορούμε να διακρίνουμε στρώματα με μια
ορισμένη ταχύτητα, όπου το ένα κινείται παράλληλα στο άλλο.
Θα μελετήσουμε την δυναμική της ποσότητας του ρευστού
που περικλείεται σε ομοαξονικό κύλινδρο ακτίνας r. Στο σχήμα έχουν σχεδιαστεί
οι δυνάμεις F1 και F2, λόγω πίεσης από τις διπλανές
ποσότητες ρευστού και η δύναμη εσωτερικής τριβής Τ, η οποία ασκείται σε όλη την
παράπλευρη επιφάνεια του μικρού κυλίνδρου. Για τα μέτρα των δυνάμεων έχουμε:
Διαβάστε τη συνέχεια:
ή
Ετικέτες
2.1 Ρευστά.,
Διονύσης Μάργαρης
Δευτέρα 27 Ιουλίου 2015
Οι ρευματικές γραμμές είναι τροχιές των υλικών σημείων του ρευστού ή όχι;
Μελετώντας την κίνηση ενός ρευστού κατά Lagrange ενδιαφερόμαστε
για την περιπέτεια κάθε ξεχωριστού αλλά τυχαίου υλικού σημείου του ρευστού.
Άλλωστε σε αυτό θα εφαρμόσουμε τον θεμελιώδη νόμο της δυναμικής.
Σχεδόν σε αντιδιαστολή με τον Lagrange ο Euler κάνει
θεωρία πεδίου. Αδιαφορεί για την περιπέτεια κάθε υλικού σημείου και
ενδιαφέρεται για την κατανομή των ταχυτήτων των σημείων του ρευστού στο χώρο
και τον χρόνο.
Με τους δύο παραπάνω ισοδύναμους τρόπους μελέτης της κίνησης
ενός ρευστού είναι συσχετισμένα δυο διαφορετικά είδη καμπυλών. Οι τροχιές των
υλικών σημείων του ρευστού και οι δυναμικές γραμμές του πεδίου.
Στην παρούσα εργασία αποδεικνύεται ότι στην μόνιμη ροή οι
δύο γεωμετρικές έννοιες ταυτίζονται.
Ετικέτες
2.1 Ρευστά.,
Βαγγέλης Κορφιάτης
Σάββατο 25 Ιουλίου 2015
Μόνιμη και μη μόνιμη στρωτή ροή.
Η ανάρτηση είναι μόνο για καθηγητές.
Στο διπλανό σχήμα εμφανίζονται
οι ρευματικές γραμμές για μια στρωτή και μόνιμη ροή νερού, το οποίο ας θεωρήσουμε
ιδανικό ρευστό, εντός ενός οριζόντιου σωλήνα. Έστω κατά μήκος μιας ευθύγραμμης ρευματικής γραμμής ένας άξονας x.
Στη θέση x=0, η πίεση είναι p0=2∙105Ν/m2, ενώ
η πυκνότητα του νερού είναι ρ=1.000kg/m3.
i) Αν η
ταχύτητα ροής του νερού κατά μήκος του άξονα δίνεται από την εξίσωση υ=1+2x
(S.Ι.), να υπολογιστούν η ταχύτητα και η επιτάχυνση ενός σωματιδίου νερού,
καθώς και η πίεση στη θέση x=2m.
ii) Αν η ροή
δεν είναι μόνιμη, αφού η ταχύτητα σε κάθε θέση x, δίνεται από την εξίσωση υ=1+2x+0,2t
(S.Ι) να βρεθούν:
α) Η ταχύτητα και η επιτάχυνση ενός σωματιδίου ρευστού
στη θέση x=2m σε συνάρτηση με το χρόνο.
β) Η πίεση στη θέση x=2m σε συνάρτηση με το χρόνο.
ή
Ετικέτες
2.1 Ρευστά.
Σάββατο 4 Ιουλίου 2015
Ιδανικά ασυμπίεστα ρευστά
Το
συνημμένο αρχείο είναι
το αποτέλεσμα της προσωπικής μου μελέτης στην προσπάθειά μου να καταλάβω την
μηχανική των ρευστών. Ουσιαστικά πρόκειται για μετάφραση μέρους του πρώτου
κεφαλαίου του βιβλίου «Fluid Mechanics» των L.D. Landau & E.M.
Lifshitz.
Η εικόνα που ακολουθεί απεικονίζει τις ρευματικές γραμμές σε ένα
αρχικά ακίνητο ρευστό μέσα στο οποίο κινείται μια σφαίρα.
Ετικέτες
Βαγγέλης Κορφιάτης,
Ρευστά
Πέμπτη 2 Ιουλίου 2015
Δυνάμεις αλληλεπίδρασης μεταξύ τροχαλίας και νήματος ή ιμάντα που την περιβάλλει
Όλοι είμαστε εξοικειωμένοι με προβλήματα, όπου ένα αβαρές μη εκτατό
νήμα ή εύκαμπτος ιμάντας περιβάλλει μια τροχαλία, δίσκο, κλπ. και δημιουργεί
ένα σύνδεσμο κίνησης αν δεν ολισθαίνει, ή έστω μια σύζευξη ανάμεσα σε δύο
σώματα, μεταφέροντας ενέργεια από το ένα στο άλλο. Το σύστημα «τροχαλίες / ιμάντας»
αποτελεί, ένα από τα συνηθισμένα συστήματα μετάδοσης κίνησης.
Σε όλες τις περιπτώσεις θεωρούμε ότι το νήμα ή ο ιμάντας ασκεί στην τροχαλία δύο «τάσεις» εφαπτομενικά
στα σημεία που έρχεται σε επαφή με αυτήν και προφανώς αυτή που είναι ομόρροπη
προς την περιστροφή προσφέρει ενέργεια στην τροχαλία, ενώ η άλλη αφαιρεί.
Με ποιο μηχανισμό ασκούνται όμως αυτές οι δύο «τάσεις»; Δεν πρόκειται για άκρο
τεντωμένου νήματος δεμένου σε σώμα. Το νήμα δεν είναι δεμένο στην τροχαλία,
απλά την περιβάλλει, βρίσκεται σε επαφή με την περιφέρειά της.
Ετικέτες
3. Στερεό,
Διονύσης Μητρόπουλος
Τρίτη 9 Ιουνίου 2015
Το Σώμα η
Ράβδος και η
Επαφή τους…
 Η παρούσα
ανάρτηση
αναφέρεται
στις
προϋποθέσεις
που πρέπει να
ισχύουν ώστε
ένα σώμα μάζας m όταν
βρίσκεται πάνω
σε μια ράβδο να
χάσει την επαφή
του με αυτή
όταν το
σύστημα αφεθεί
ελεύθερο να κινηθεί.
Κατόπιν αν σε
κάποιο στάδιο
κατά τη
διάρκεια των
κινήσεων των
σωμάτων της
ράβδου και του
σφαιριδίου μπορεί
το σφαιρίδιο m να συναντηθεί
με τη ράβδο και
υπό ποιες
προϋποθέσεις επιτυγχάνεται
αυτό.
Η παρούσα
ανάρτηση
αναφέρεται
στις
προϋποθέσεις
που πρέπει να
ισχύουν ώστε
ένα σώμα μάζας m όταν
βρίσκεται πάνω
σε μια ράβδο να
χάσει την επαφή
του με αυτή
όταν το
σύστημα αφεθεί
ελεύθερο να κινηθεί.
Κατόπιν αν σε
κάποιο στάδιο
κατά τη
διάρκεια των
κινήσεων των
σωμάτων της
ράβδου και του
σφαιριδίου μπορεί
το σφαιρίδιο m να συναντηθεί
με τη ράβδο και
υπό ποιες
προϋποθέσεις επιτυγχάνεται
αυτό.Δευτέρα 1 Ιουνίου 2015
Ολίσθηση σφαίρας σε ημισφαίριο
Από το χείλος ενός στερεωμένου ημισφαιρίου, μια σφαίρα
ακτίνας r αφήνεται ελεύθερη
να κινηθεί όπως στο σχήμα
Στην αρχή η κίνηση της σφαίρας είναι ολίσθηση και κάποια
στιγμή μετατρέπεται σε κύλιση χωρίς ολίσθηση.
Να αποδείξετε ότι, για αρκούντως μεγάλες τιμές του
συντελεστή τριβής μεταξύ των υλικών της σφαίρας και του ημισφαιρίου, η ενέργεια που μετατρέπεται σε θερμική είναι
αμελητέα.
Εισαγωγή
Η διερεύνηση του παραπάνω προβλήματος γίνεται με αφορμή το
θέμα Δ1 των πανελλαδικών εξετάσεων του 2015.
Είναι γνωστό ότι, ανεξαρτήτως της τιμής του συντελεστή
τριβής, αφήνοντας την σφαίρα στο σημείο Α, υπάρχει ένα χρονικό διάστημα στο
οποίο η σφαίρα ολισθαίνει μέχρι να ικανοποιηθεί η συνθήκη κύλισης υcm=ωr.
Διαισθητικά περιμένουμε ότι αυξανομένου του συντελεστή
τριβής το χρονικό διάστημα και το διανυόμενο τόξο αποκατάστασης τείνουν στο
μηδέν καθιστώντας το μοντέλο «από την πρώτη στιγμή κυλίεται χωρίς να
ολισθαίνει» σχεδόν αποδεκτό.
Υπάρχει ένας προβληματισμός σχετικά με την ενέργεια που
μετατρέπεται σε θερμική κατά την διάρκεια της αποκατάστασης: Αυξανομένου του
συντελεστή τριβής αυξάνεται το μέτρο της τριβής και μειώνεται το μήκος του
διανυόμενου τόξου. Από πρώτη ματιά είναι απροσδιόριστο το γινόμενο τριβή x απόσταση.
Ετικέτες
3. Στερεό,
Βαγγέλης Κορφιάτης
Κυριακή 24 Μαΐου 2015
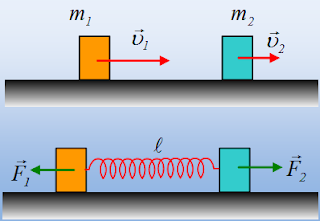
Οι μετατοπίσεις σε μια ελαστική κρούση και το cm.
Σε λείο οριζόντιο επίπεδο
κινούνται προς την ίδια κατεύθυνση δύο σώματα με μάζες m1=2kg, m2=3kg
και ταχύτητες υ1=10m/s και υ2=5m/s. Σε μια στιγμή
συγκρούονται μετωπικά και ελαστικά. Θεωρούμε ότι η ελαστική αυτή κρούση,
προσομοιάζεται με την αλληλεπίδραση των δύο σωμάτων, μέσω ενός ελατηρίου,
σταθεράς k=3.000Ν/m και φυσικού μήκους l0=1m, όπου το ελατήριο αυτό
είναι προσαρμοσμένο στο πίσω μέρος του σώματος m2, πάνω στο άλλο
άκρο του οποίου προσπίπτει το σώμα m1.
Να υπολογιστούν οι μετατοπίσεις των δύο σωμάτων στη διάρκεια της κρούσης.
Ετικέτες
1. Ταλαντώσεις,
4.Κρούση,
Διονύσης Μάργαρης
Πέμπτη 23 Απριλίου 2015
Παίζοντας με μια ερώτηση
Πριν λίγες μέρες ο Διονύσης, ο Βασίλης και ο Χρήστος είχαν
απαντήσει σε ερώτηση του Παναγιώτη Γκρέευ. Παραλλάσσοντας την άσκηση παίζω μ’
αυτήν.
Η καφέ σανίδα έχει μάζα 2kg. Το ίδιο και το κόκκινο σώμα.
Η σταθερά του ιδανικού ελατηρίου είναι 50 Ν/m.
Αρχικά η σανίδα είναι ακίνητη και το κόκκινο σώμα έχει
ταχύτητα 2 m/s.
Τριβές δεν υπάρχουν.
Τριβές δεν υπάρχουν.
1. Ποια θα είναι η μέγιστη συσπείρωση του ελατηρίου;
2. Πόσος χρόνος μεσολάβησε ώστε αυτή να επιτευχθεί;
3. Πόσο έχει μετατοπισθεί κάθε σώμα μέχρι αυτήν την στιγμή;
Πέμπτη 19 Μαρτίου 2015
Μια ακόμη πιο …δύσκολη συνέχεια.
Μόνο για καθηγητές.
Σαν συνέχεια της ανάρτησης «Μια ...δύσκολη
περίπτωση, σαν φύλλο εργασίας.» ας δούμε μερικά ακόμη ερωτήματα,
αφήνοντας όμως έξω τους μαθητές-υποψήφιους.
Ένα ορθογώνιο μήκους l (σώμα
Σ), μάζας Μ=40kg κινείται σε λείο οριζόντιο επίπεδο. Σε μια στιγμή, αφήνουμε
πάνω του, μια σφαίρα μάζας m=20kg και ακτίνας R=0,2m, χωρίς να έχει αρχική ταχύτητα
ούτε να περιστρέφεται. Μετά από λίγο, τη στιγμή t1, το σώμα Σ έχει
ταχύτητα υσ=4m/s, η ταχύτητα του κέντρου της σφαίρας είναι υcm=1m/s,
ενώ το σημείο επαφής της Γ με το Σ, απέχει οριζόντια κατά (ΜΓ)= d=0,6m από το μέσον Μ του
ορθογωνίου (σχήμα α).
Δίνεται η ροπή αδράνειας της σφαίρας ως προς άξονα που
περνά από το κέντρο της Ι= 2/5 mR2 και g=10m/s2, ενώ ο συντελεστής τριβής μεταξύ σφαίρας και σανίδας είναι
μ=0,5.
1) Αν το σώμα
Σ είναι μια λεπτή σανίδα, να υπολογιστεί η στροφορμή και ο ρυθμός μεταβολής της
στροφορμής, τη παραπάνω στιγμή:
α) για το σύστημα,
β) για τη σφαίρα, γ) για τη
ράβδο.
i) Ως προς ένα
ακίνητο σημείο Γ1, στη θέση που είναι και το σημείο Γ της σανίδας.
ii) Ως προς ακίνητο σημείο Μ1 στη θέση του
μέσου Μ της σανίδας:
iii) Ως προς ακίνητο σημείο Ο1 στη θέση του
κέντρου Ο της σφαίρας:
2) Αν το ορθογώνιο είναι κιβώτιο σχήματος ορθογωνίου
παραλληλεπιπέδου (σχήμα β), ύψους h=0,6m να απαντήσετε ξανά στα παραπάνω
ερωτήματα.
ή
Ετικέτες
3. Στερεό,
Διονύσης Μάργαρης
Κυριακή 1 Μαρτίου 2015
Δύο μπάλες μπιλιάρδου συγκρούονται
Συγκρούονται μετωπικά με ταχύτητες όπως στο σχήμα. Η μεταξύ
τους τριβή είναι αμελητέα.
Ο συντελεστής τριβής μεταξύ τσόχας και μπίλιας είναι μ =
0,5.
Ποιες θα είναι οι τελικές τους ταχύτητες;
Σε πόσο χρόνο κάθε μπίλια θα αποκτήσει την τελική της
ταχύτητα;
Δευτέρα 23 Φεβρουαρίου 2015
Περισσότεροι κινηματικοί περιορισμοί.
Αποκλειστικά και
μόνο για Καθηγητές.
Αφήνουμε μια σκάλα ύψους 2m σε επαφή με λείο κατακόρυφο
τοίχο και σε τέτοια θέση, ώστε να σχηματίζει με το έδαφος γωνία θ, όπου
ημθ=0,8. Η σκάλα αρχίζει να γλιστρά, αφού και το έδαφος είναι επίσης λείο.
Να βρεθεί η αρχική επιτάχυνση του μέσου Κ της σκάλας
και η αρχική γωνιακή επιτάχυνση της σκάλας, στην παραπάνω θέση.
Θεωρείστε τη σκάλα σαν μια ομογενή δοκό, για την οποία
η ροπή αδράνειας, ως προς κάθετο άξονα που περνά από το μέσον της, δίνεται από
τη σχέση Ι= Μl2/12, ενώ g=10m/s2.
ή
Ετικέτες
3. Στερεό,
Διονύσης Μάργαρης
Κυριακή 8 Φεβρουαρίου 2015
Παίζοντας με το 2ο νόμο για την περιστροφική κίνηση.
Αποκλειστικά και μόνο για Καθηγητές.
Κάθε χρόνο επανέρχεται στο προσκήνιο το θέμα εφαρμογής
του 2ου νόμου για την στροφική κίνηση και η αποφυγή χρήσης του, σε
περίπτωση λανθασμένης εφαρμογής.
Ας διερευνήσουμε τα όρια λοιπόν εφαρμογής του, μέσα από
κάποια παραδείγματα εφαρμόζοντάς τον σε ένα πρόβλημα, ως προς διαφορετικά
σημεία.
Το πρόβλημα:
Ένας κύλινδρος ακτίνας R=20cm και μάζας 2kg, κινείται
σε οριζόντιο επίπεδο με την επίδραση στον άξονά του οριζόντιας δύναμης F=16Ν,
ενώ η ασκούμενη τριβή ολίσθησης έχει μέτρο Τ= ¼ F= 4Ν. Η ροπή αδράνειας του κυλίνδρου
δίνεται από την εξίσωση Ι= ½ mR2. Να βρεθεί η γωνιακή επιτάχυνση του
τροχού.
Απάντηση:
i)
Ο γνωστός σε όλους τρόπος, είναι να
θεωρήσουμε σύνθετη την κίνηση, αποτελούμενη από μια μεταφορική και μια στροφική
γύρω από τον άξονα του κυλίνδρου, άξονας που περνά και από το κέντρο μάζας Ο
του κυλίνδρου.
Η συνέχεια σε pdf.
Ετικέτες
3. Στερεό,
Διονύσης Μάργαρης
Σάββατο 7 Φεβρουαρίου 2015
Η σανίδα και ο τροχός Νο2
Η
σανίδα του σχήματος έχει μάζα 20
kg και μήκος 4m.
Ο τροχός έχει μάζα επίσης 20 kg και ακτίνα 0,5m.
Το κέντρο μάζας του συστήματος έχει σημειωθεί ώστε ο
αναγνώστης να απαλλαγεί από την φασαρία του προσδιορισμού του.
Μπορούμε ασκώντας μόνο οριζόντια δύναμη στο άκρο Α να
αναγκάσουμε την σανίδα να κινείται παραμένουσα οριζόντια;
Ο τροχός δεν ολισθαίνει.
Η σανίδα και ο τροχός. Μια σπαζοκεφαλιά.
Ο τροχός έχει μάζα επίσης 20 kg και ακτίνα 0,5m.
Το κέντρο μάζας του συστήματος έχει σημειωθεί ώστε ο
αναγνώστης να απαλλαγεί από την φασαρία του προσδιορισμού του.
Ποια δύναμη πρέπει να δέχεται στο άκρο Α ώστε να κινείται με
σταθερή επιτάχυνση 2 m/s2 , παραμένοντας
οριζόντια;
Παρασκευή 2 Ιανουαρίου 2015
Ακρότητες. Μια άσκηση τραβηγμένη λύνεται ενεργειακά.
Σας δίνουν ένα πρόβλημα όπως:
Δείξτε
ότι κάνει ταλάντωση, υπολογίσατε θέση ισορροπίας, περίοδο κ.λ.π.
Δεδομένο ας θεωρηθεί το ότι δεν ολισθαίνει ουδέν επί
ουδενός.
Το πρόβλημα σας το έδωσε κάποιος με μια λύση που το
συνοδεύει και θέλετε να το ελέγξετε.
Θεωρείτε ακρότητα το παραπάνω πρόβλημα και δεν σκέφτεστε να
το κάνετε στον πίνακα. Εν τούτοις θέλετε μια λύση. Αν σημειώσετε τις δυνάμεις
και πάρετε τις γνωστές εξισώσεις θα το λύσετε σίγουρα.
Ας δούμε μια ενεργειακή λύση.
Εγγραφή σε:
Αναρτήσεις (Atom)