Το φαινόμενο φθίνουσα ταλάντωση, λόγω δύναμης απόσβεσης της μορφής F=-bυ, ισχύει μόνο αν 0 < b2 <4Dm ή 0 < Λ < ω0 και έγινε πλέον σαφές από τις αναρτήσεις του καλοκαιριού στο blog του Δ. Μάργαρη αλλά και στο δίκτυο «Διδάσκοντας Φυσικές Επιστήμες» ότι οι σχέσεις Α = Α0 e -Λt και Ε = Ε0 e -2Λt που χρησιμοποιούσαμε για να περιγράφουμε το πλάτος και την ενέργεια αντίστοιχα στην φθίνουσα ταλάντωση είναι πάντα ΛΑΘΟΣ. (Δεν αναφέρομαι αναλυτικά στο φαινόμενο γιατί έχουν ήδη γραφεί πολλά).
Μετά το αρχικό σοκ, που για αρκετούς ήταν πάρα πολύ ισχυρό, το να επιχειρήσουμε να δικαιολογήσουμε τους προηγούμενους λανθασμένους τύπους, χρησιμοποιώντας όχι πλέον εκείνο το αμίμητο και τελείως αόριστο επιχείρημα “… ισχύουν όταν είναι μικρή η σταθερά απόσβεσης b ” αλλά το καινούριο “… ισχύουν όταν Λ << ω0” έχω την εντύπωση ότι προσπαθούμε να ορίσουμε και να περιγράψουμε ένα νέο φαινόμενο σαν «υποπερίπτωση» της φθίνουσας ταλάντωσης, την οποία εξοστρακίζουμε και πάλι.
Με τέτοιες λογικές όμως χάνουμε από την προσοχή μας τα φυσικά φαινόμενα, για να σώσουμε ντε και καλά λανθασμένες σχέσεις τις οποίες θα χρησιμοποιούμε για να λύνουμε ασκήσεις. Και γιατί άραγε θα πρέπει να στριμωχτούμε στην υποπερίπτωση Λ << ω0 και να μην ανακαλύψουμε και μια ακόμη «υποπερίπτωση» της φθίνουσας ταλάντωσης που ισχύει όταν το Λ πλησιάζει το ω0 από αριστερά;
Ποιό θα είναι όμως το όφελος αν περιγράψουμε ένα φαινόμενο προσεγγιστικά σε μια πολύ μικρή περιοχή τιμών από αυτές του μοναδικού περιορισμού 0 < Λ < ω0 που υποχρεωτικά ισχύει για να έχουμε φθίνουσα ταλάντωση; Και γιατί το ενδιαφέρον μας να είναι σε μια μικρή περιοχή τιμών και μόνο ως προς το κάτω όριο του περιορισμού, δηλαδή για Λ αρκετά μικρότερο από την ω0 (Λ<< ω 0) και όχι ενδεχομένως και ως προς το πάνω όριο δηλαδή Λ σχεδόν ίσο με την ω; Τι σημαίνει άραγε Λ πολύ μικρότερο από την ω0 ; Πόσο μικρότερο δηλαδή; Τριάντα φορές, πενήντα, εκατό φορές; Ή μήπως είναι λίγο; Ποιος θα ορίσει αυτό το πόσο; Ή μάλλον πόσοι θα χαθούν και θα λαθέψουν από αυτό το αόριστο πόσο;
Γιατί άραγε τα συμπεράσματα που θα προκύψουν «προσεγγιστικά» από αυτή την μικρή περιοχή τιμών να πρέπει να επιβληθούν των γενικών συμπερασμάτων του φαινομένου.
Να το πω και με άλλα λόγια:
Η προσέγγιση ενός φαινομένου μπορεί να σε οδηγήσει σε συμπεράσματα που αν τα χρησιμοποιήσεις για να περιγράψεις το φαινόμενο συνολικά θα είναι αντιφατικά με το ίδιο το φαινόμενο.
Για να καταλάβουμε τις συνέπειες τέτοιων προσεγγίσεων που μας αποπροσανατολίζουν έτσι ώστε να χάνουμε το πραγματικό φυσικό φαινόμενο (σαν να χάνουμε το δάσος και να βλέπουμε το δέντρο) και να βλέπουμε μια «υποπερίπτωση» του φαινομένου, θα χρησιμοποιήσω ένα παράδειγμα από την ευθύγραμμη κίνηση ενός σώματος, όπου με την ίδια προσεγγιστική λογική οδηγεί σε άλλες σχέσεις κόντρα στις σωστές.
Η εξίσωση θέσης στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση (Ε.Ο.Επιτ.Κ.) είναι η:
x = x0 + υ0 (t-t0) + 1/2 a (t-t0)2
Ο υποθετικός καθηγητής κ. Βραχάκης προτείνει ότι, όταν η επιτάχυνση είναι αρκετά μικρή και μελετάμε τη κίνηση από τη χρονική στιγμή t=0 και για ένα επόμενο μικρό χρονικό διάστημα, να την περιγράφει η
x = x0 + υ0 (t-t0)
Για να μας πείσει ότι έχει δίκαιο παραθέτει τις παρακάτω γραφικές παραστάσεις x-t :
α) μιας Ε.Ο.Επιτ.Κ. με αρχική θέση x0 = 2 m και υ0 = 2 m/s όταν η επιτάχυνση είναι μεγάλη α = 1 m/s2 και όταν είναι μικρή α = 0,02m/s2 ή ακόμη πιο μικρή α = 0,01m/s2
β) μιας ευθύγραμμης ομαλής κίνησης (Ε.Ο.Κ.) με ίδιες αρχικές συνθήκες, δηλαδή με αρχική θέση x0 = 2 m και υ0 = 2 m/s
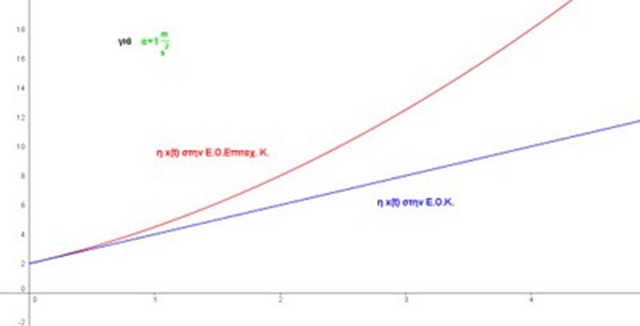

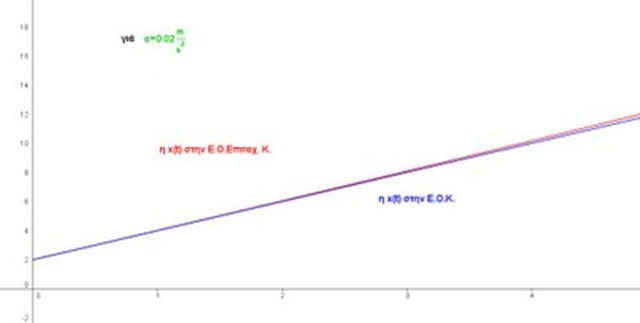
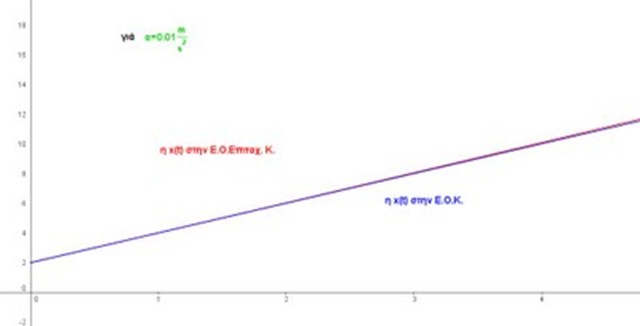
Ο καθηγητής κύριος Βραχάκης με δεδομένη την ταύτιση των γραφικών παραστάσεων στα τελευταία διαγράμματα επιμένει ότι η εξίσωση θέσης στην Ε.Ο.Επιτ.Κ. είναι η x = x0 + υ0 (t-t0) αρκεί η επιτάχυνση να είναι αρκετά μικρή.
Επιστρέφοντας στο φαινόμενο της φθίνουσας ταλάντωσης η προσέγγιση «… όταν ισχύει Λ<< ω είναι ικανή να σώσει τους τύπους» (και γιατί να τους σώσει άραγε;) δεν είναι ικανοποιητική. Η γνώμη μου είναι να συμφωνήσουμε ότι αφού οι σχέσεις είναι λάθος δεν πρέπει να ξαναχρησιμοποιηθούν για να περιγράψουν αυτά που νομίζαμε μέχρι χθες ότι περιέγραφαν (αυτό όσον αφορά την ακρίβεια του φαινομένου).
Όσον αφορά τη διδασκαλία στους μαθητές θα ήταν μια καλή αρχή να ζητηθεί από το Π.Ι. και το υπουργείο παιδείας να εξαιρεθεί η διδασκαλία των φθινουσών ταλαντώσεων ή τέλος πάντων να γίνεται σε ποιοτικό αποκλειστικά επίπεδο χωρίς κανένα τύπο και σε μια νέα έκδοση του σχολικού να αφαιρεθούν από τις σελίδες του ή να διορθωθούν.
Για μία ποιο οπτικοποιημένη εξήγηση όσων υποστηρίζω έχω σχεδιάσει τη γραφική παράσταση της ενέργειας σε συνάρτηση με το χρόνο για τον συνδυασμό τιμών D = 1000Ν/m, m = 0,4Kg επομένως ω = 50 rad/s και Λ=0,5 s-1 δηλαδή να ισχύει Λ<< ω ( η Λ είναι εκατό φορές μικρότερη της ω0). Παρατηρείστε πόσο μειώνεται η τιμή της ενέργειας μέσα στην πρώτη κιόλας περίοδο καθώς και πόσο διαφορετικές είναι οι τιμές της ενέργειας οποιαδήποτε χρονική στιγμή από αυτές που υπολογίζει η σχέση Ε = Ε0 e -2Λt. Τίποτα δεν δικαιώνει την έκφραση «…για μικρές αποσβέσεις η μείωση της ενέργειας είναι πολύ αργή»
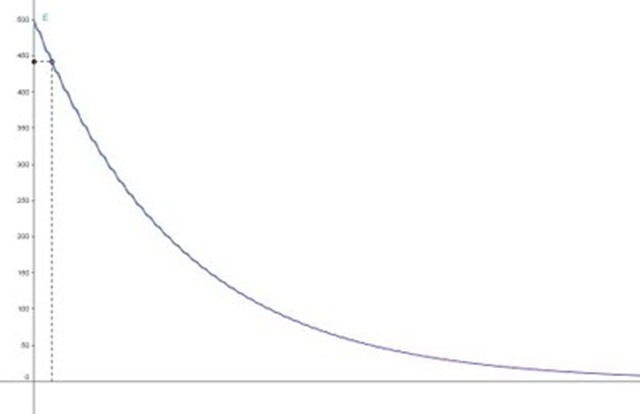
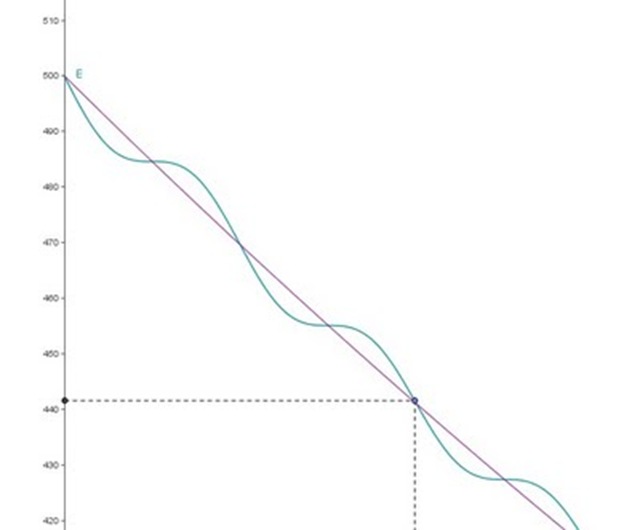


(Λεπτομέρεια της προηγούμενης γραφικής παράστασης)
Αν συμβαίνει αυτή η «προσεγγιστικά» αργή μείωση της ενέργειας συμβαίνει μόνο μετά την πραγματοποίηση αρκετών ταλαντώσεων και για το χρονικό εκείνο διάστημα που οι διακυμάνσεις της ενέργειας είναι μικρές και η εκθετική συνάρτηση ασυμπτωτικά έχει πλησιάσει τον άξονα των χρόνων. Αλλά όχι πάντα.
Γιατί λοιπόν συμπεράσματα που προκύπτουν «προσεγγιστικά» από μικρές περιοχές τιμών, να πρέπει να επιβληθούν των γενικών συμπερασμάτων του φαινομένου; Δεν το καταλαβαίνω.
Σταύρος Λέτης




