Στην προηγούμενη ανάρτηση με τίτλο Στροφορμή, είχαμε ορίσει την στροφορμή υλικού σημείου ως προς σημείο Ο, από την σχέση:
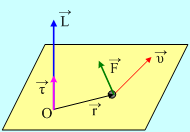
![clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiz9iaGW-6SMdHiQyr3zrGoCGH5tokFZx0aKAGm8tRo7xMeNcvb1wLu4xuAJIpe9_oqz9-q0JNMW-STvf1v_GKV5C1KwpFlc8UBXwl50lEpSw_UAlb3vc6bisZLeemWkaAZ3aNv0dQ4hGg/?imgmax=800)
Εφαρμογή 1η:
Από σημείο Ο σε ύψος Η=20m, εκτοξεύεται για t=0 οριζόντια ένα μικρό σώμα, μάζας m=0,1kg με αρχική ταχύτητα υ0=10m/s. Για τη χρονική στιγμή t1=1s, ζητούνται:
α) Η στροφορμή του σώματος ως προς το σημείο Ο.
β) Ο ρυθμός μεταβολής της στροφορμής του σώματος ως προς το Ο.
Δίνεται g=10m/s2.
Απάντηση:
Για την οριζόντια βολή και για τις κινήσεις πάνω
 στους άξονες x και y, του διπλανού σχήματος, ισχύουν οι εξισώσεις:
στους άξονες x και y, του διπλανού σχήματος, ισχύουν οι εξισώσεις:υx= υ0 , υy=g∙t, x=υ0∙t και y= ½ gt2.
Έτσι για t=1s παίρνουμε:
υy= 10m/s, x=10m και y=5m.
Οπότε το σώμα έχει φτάσει στο σημείο Α με ταχύτητα μέτρου υ=10√2m/s που σχηματίζει γωνία θ=45° με την οριζόντια διεύθυνση.
Ποια είναι η στροφορμή του σώματος ως προς το σημείο Ο;
Είναι διάνυσμα κάθετο στο επίπεδο της τροχιάς (επίπεδο της σελίδας) με φορά προς τα μέσα και μέτρο:
L= mυr∙ημφ
Όπου φ η γωνία μεταξύ των διανυσμάτων  r και υ.
r και υ.Αλλά με βάση το σχήμα ημφ= d/r έχουμε:
L=mυd
Όπου d η απόσταση του φορέα της ταχύτητας στο σημείο Α, από το σημείο Ο.Αλλά με βάση τη Γεωμετρία, το τρίγωνο ΟΒΓ είναι ορθογώνιο και ισοσκελές, ενώ (ΓΔ)=(ΔΑ)=y=5m συνεπώς και (ΟΓ)=5m, οπότε d2+d2=(OΓ)2 άρα d=5/√2m και με αντικατάσταση στην (1) L=5 kgm2/s.
Έχει φασαρία;
Ας το ξαναδοκιμάσουμε:
Η στροφορμή του υλικού σημείου ως προς το Ο, είναι το διανυσματικό άθροισμα της στροφορμής εξαιτίας της ταχύτητας υx και της στροφορμής εξαιτίας της υy. Όπου και οι δύο αυτές συνιστώσες είναι κάθετες στο επίπεδο, η Lx θετική, ενώ η Ly αρνητική:
Άρα L=mυxy – mυyx
Και με αντικατάσταση L=5kgm2/s.

To τελευταίο αποτέλεσμα μας λέει ότι το διάνυσμα της στροφορμής είναι κάθετο στο επίπεδο (άξονας z) και με φορά προς τα μέσα.
β) Ο ρυθμός μεταβολής της στροφορμής του σώματος ως προς το σημείο Ο είναι:
dL/dt= -w∙x = -mgx
και με αντικατάσταση dL/dt= -10kgm2/s2.Και αυτό το διάνυσμα είναι κάθετο στο επίπεδο με φορά προς τα μέσα.
Εφαρμογή 2η:
Ένα υλικό σημείο μάζας 0,2kg κρέμεται στο άκρο νήματος μήκους l=√2m.

Εκτρέπουμε το σώμα φέρνοντάς το στη θέση Α, όπου το νήμα σχηματίζει γωνία θ=45° με την κατακόρυφο και το αφήνουμε να κινηθεί. Να βρεθεί ο αρχικός ρυθμός μεταβολής της στροφορμής του σώματος, ως προς άκρο Ο του νήματος.
Δίνεται g=10m/s2.
Απάντηση:
Το σώμα θα εκτελέσει επιταχυνόμενη κυκλική κίνηση με κέντρο το Ο και ακτίνα l και ο αρχικός ρυθμός μεταβολής της στροφορμής, θα είναι κάθετος στο επίπεδο της τροχιάς, με φορά προς τα έξω και μέτρο:
dL/dt=ΣτΟ=+mgd=mgl∙ημθ
και με αντικατάσταση dL/dt=2kgm2/s2.Εφαρμογή 3η:
Το σώμα της προηγούμενη εφαρμογής από τη θέση Α εκτοξεύεται με οριζόντια ταχύτητα, τέτοια ώστε να διαγράφει οριζόντια κυκλική τροχιά ακτίνας r=d=1m (οπότε το νήμα διαγράφει την παράπλευρη επιφάνεια ενός κώνου).
Ζητούνται:
α) Η ταχύτητα υ.
β) Η στροφορμή του σώματος ως προς το σημείο Ο.
γ) Η προβολή της στροφορμής του σώματος πάνω στον κατακόρυφο άξονα z που περνά από το κέντρο Κ της κυκλικής τροχιάς (η στροφορμή κατά τον άξονα z).
δ) Ο ρυθμός μεταβολής της στροφορμής ως προς το Ο.

Απάντηση:
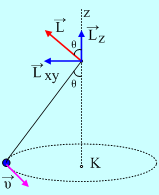
α) Με βάση το διπλανό σχήμα έχουμε:
ΣFy=0 → T συνθ=mg (1)
ΣFx=mυ2/r → Τημθ = mυ2/r (2)
Από (1) και (2) παίρνουμε:
Και με αντικατάσταση:
Καθώς το σώμα περιστρέφεται και το διάνυσμα της στροφορμής στρέφεται διαγράφοντας την παράπλευρη επιφάνεια ενός κατακορυφήν κώνου, αυτού που διαγράφει το νήμα.
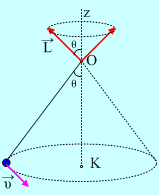
δ) Για τον ρυθμό μεταβολής της στροφορμής ως προς το σημείο Ο έχουμε:
dL/dt=Στ= mgd
και με αντικατάσταση dL/dt=2kgm2/s2.Με διεύθυνση κάθετη στο επίπεδο που ορίζει η διεύθυνση του βάρους (κατακόρυφη) και το σημείο Ο, συνεπώς οριζόντια διεύθυνση.
Σχόλια:
1) Η στροφορμή του σώματος μεταβάλλεται, αφού αλλάζει κατεύθυνση, παρότι διατηρεί σταθερό το μέτρο της. Η συνιστώσα όμως της στροφορμής πάνω στον άξονα z, γύρω από τον οποίο στρέφεται το στερεό, δεν μεταβάλλεται. Μεταβάλλεται μόνο η οριζόντια συνιστώσα της στροφορμής, αφού διαγράφει οριζόντιο κύκλο.
Πράγματι ας δούμε τον κύκλο που διαγράφει η
![clip_image002[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjBtOT5GFmQwA_1Qde1eItTQjZkgdH90-pl2MBdfQkd6zMmGC-gpdCmGxQCyYjg495z-rjX_hkgy9wmMLolCvwPnjaZC1gvAhTIKBfScU4b5Sb9mzQpJE4wbwrIC-oMIiJn1fSMTpwjg3g/?imgmax=800) οριζόντια συνιστώσα.
οριζόντια συνιστώσα.Αν για t=0 η οριζόντια συνιστώσα της στροφορμής είναι η L1, μετά από χρόνο dt θα έχουμε
2) Αν συγκρίνουμε το αποτέλεσμα της εφαρμογής 2 με αυτό της εφαρμογής 3δ, παρατηρούμε ότι και στις δύο περιπτώσεις έχουμε τον ίδιο ρυθμό μεταβολής της στροφορμής, πράγμα αναμενόμενο αφού στο σώμα ασκείται η ίδια ροπή (του βάρους). Και όμως στην πρώτη περίπτωση το σώμα κινείται προς τα κάτω διαγράφοντας κατακόρυφο κύκλο, ενώ στην δεύτερη περίπτωση δεν συμβαίνει αυτό, αφού ο διαγραφόμενος κύκλος είναι οριζόντιος.
3) Ας μεταφέρουμε το παραπάνω συμπέρασμα,
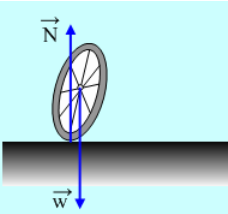 σε μια ρόδα ποδηλάτου. Αν την αφήσουμε όρθια και ακίνητη εξαιτίας της ροπής* του ζεύγους βάρος-κάθετη αντίδραση του επιπέδου, εκτρέπεται και πέφτει.
σε μια ρόδα ποδηλάτου. Αν την αφήσουμε όρθια και ακίνητη εξαιτίας της ροπής* του ζεύγους βάρος-κάθετη αντίδραση του επιπέδου, εκτρέπεται και πέφτει.Αν όμως κινείται, πράγμα που σημαίνει ότι έχει στροφορμή οριζόντια, η αντίστοιχη ροπή του ζεύγους, θα προκαλέσει μια οριζόντια μεταβολή dL κάθετη στην αρχική στροφορμή, με αποτέλεσμα η ρόδα να «στρίβει» λίγο, χωρίς όμως να ανατρέπεται.

dmargaris@sch.gr
Μπορείτε να το κατεβάσετε σε pdf

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου